Random Test Generator - Bridging the gap
Recently we faced the task of testing software, which was a bridge between two other tools: taking the output of one and transforming it into the input of the other. The transformation was complex.
A test suite was developed manually for this transformation. However each test required the construction of a complex data structure, which limited the sizes of the tests. The problem was to develop large data structures to test the correctness and efficiency of the transformation.
To do this manually would have taken too long and been error prone. NPL has over the years developed a means to generate random self-compilers, in particular for PASCAL, (also variants), Ada and several other languages.
This article describes briefly the random self-checking program generator and how the technology used to construct it was applied to generate tests for the bridging software described above.
Background
Validation suites for compilers have been developed consisting of manually produced programs, which are used to test compilers. Unfortunately compilers can pass these and still have serious bugs in them.
The aim of the random program generators was to generate programs, which should compile and on execution perform a self-check. The basic idea is to generate very complicated constructs by recursive descent and check that these are evaluated correctly. A very simple example might be the following:
V1 : = 6;
V2 : = (4 – (2 – 1)) * ((3 * 2) / (8 mod 5));
IF V1 = V2 THEN
write1n('Test Passed')
ELSE
write1n('Test failed');
The value for V1 is chosen at random but such that it is correct in terms of its type. V2 is then assigned a value by means of a complex data structure, which is created by recursive descent from the value that V1 has been set to, in this case 6. The values of V1 can then be checked against that of V2.
The same technique can be generalised for most of the constructs of a programming language. The main technical problem is preserving the correct semantics while doing the recursive descent. This technique has produced program generators, which have found many bugs in commercial compilers and has been used to give assurance for compilers in a safety-critical context.
Application
The bridging tool forms a bridge between two commercially available tools, NP-Tools (available from Prover Technology AB and distributed in the UK by the National Physical Laboratory) and FaultTree+ (available from IsographDirect).
NP-Tools is a tool which can be use to model the logic of systems and prove properties about the models. FaultTree+ is a reliability analysis tool, which allows you too develop fault trees and do some analysis on them.
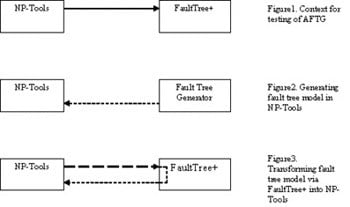
The bridge between them, is the Automatic Fault Tree Generator (AFTG), see Figure 1. Fault trees consist of logical gates. To test the AFTG fully it was required to produce fault trees of the order of 4000 gates (maximum for FaultTree+ is 5000).
To create the appropriate model in NP-Tools would be too time consuming, so it was decided to generate fault trees. The random generator technology described above was used to generate the fault trees.
The fault tree generator had to enforce two semantic properties. The first being that there existed one set of values for which the fault tree evaluated to true and the second being that there were no circularities (fault trees are allowed to refer to other parts of the tree rather than just repeat it).
To enable the results of the tests to be checked the ability of NP-Tools to prove that two logical models are equivalent was used.
A fault tree was generated automatically and placed in NP-Tools (via a converter FTtoNPT), see Figure 2. The fault tree in NP-Tools, was then transformed via AFTG into FaultTree+ and then back into NP-Tools, see Figure 3. NP-Tools can be used to prove the two fault trees are logically equivalent in which case the test has passed, if not the test has failed.
The fault tree generator was implemented in a scripting language Tcl/Tk with parameters to select size and degree of repetition within the generated fault tree.
Fault trees were generated of the order of 4000 gates. This technique was found to be very effective in testing the AFTG as the generated fault trees are more complex than would normally be produced.
Conclusion
The technique described above was very good in generating complex tests. It can be applied when the tests require complex structures, have relatively simple semantics and there is a means to check the results automatically.
Graeme Parkin, National Physical Laboratory